Answer (1 of 15) Imagine y is an apple, so if you have two apples and add another apple, how much apples do you have now?
32(x+y)2-2x-2y- x y = 2 2 x 4 y = 32 x 5 y = 34 (We used 3 given that the third new equation is a linear combination of the first and second equation The third equation is the sum of the first and the second one) In the exercise, is equivalent to Because we divided the second equation by 2 (Notice that this is an example of 2 because weAnswer (1 of 8) The equation of a circle x^2 y^2 6x 2y 8 becomes x^2 y^2 6x 2y = 8 is of the form (xh)^2 (yk)^2 = r^2, or x^2 2hx h^2 y^2 2ky k^2 = r^2 Here 2hx = 6 or h = 3, and 2ky = 2y, or k = 1 h^2 k^2 = r^2 8, or 3^2 (1)^2 = r^2 8, or 9 1
32(x+y)2-2x-2yのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  | |
 |  |  |
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  |  |
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
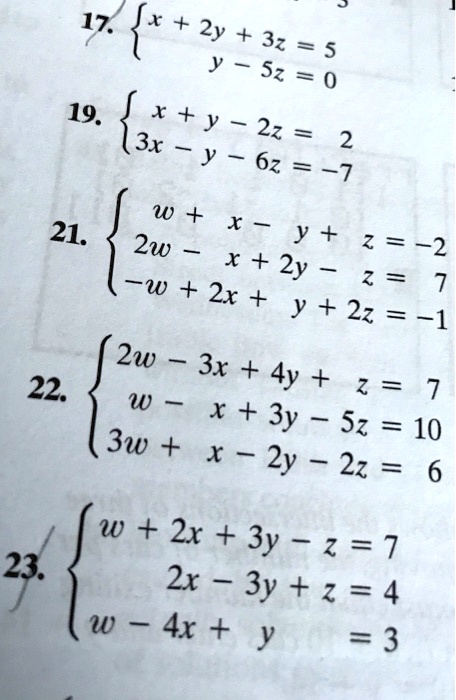 |  | |
 |  | |
 |  | |
 |  |  |
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
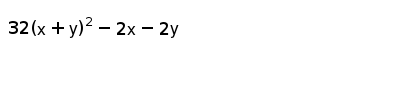 |  |  |
 |  | |
 |  |  |
 | ||
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
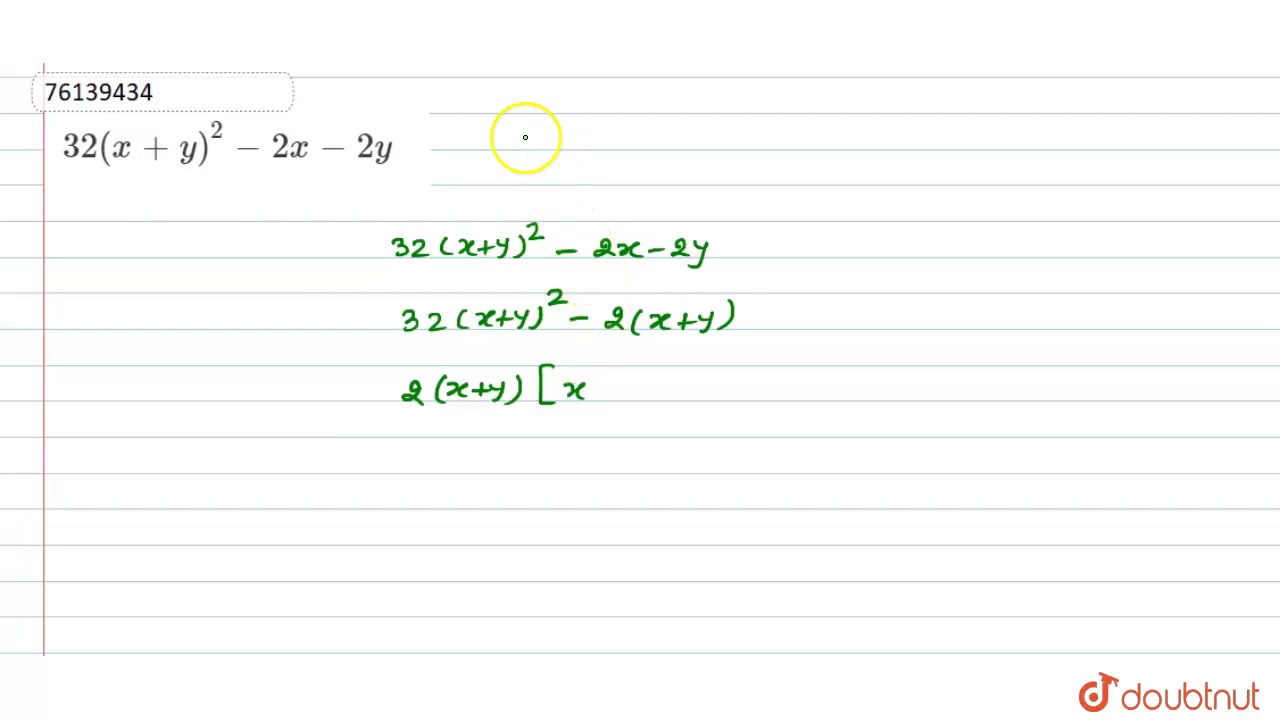 |  | |
 |  | |
 |  |  |
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  |  |
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「32(x+y)2-2x-2y」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
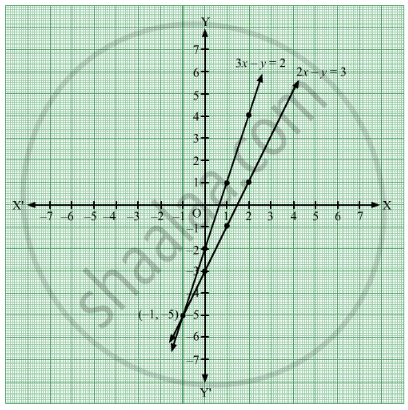
At a typical x value Such a line enters D at y = x2 and leaves at y = 2x The integral becomes ZZ D (4x2)dA = Z 2 0 Z 2x x2 (4x2)dydx = Z 2 0 4xy 2yy=2x y=x2 dx = Z 2 0 8x2 4x − 4x3 2x2 dx = Z 2 0 (6x2 −4x3 4x)dx = h 2x3 −x4 2x2 i 2 0 = 8 The example we have just done shows that it is sometimes easier to do it one way than theTo solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 3xy=2,2xy=3 3 x − y = 2, 2 x − y = 3 Choose one of the equations and solve it
Incoming Term: 32(x+y)2-2x-2y,




0 件のコメント:
コメントを投稿