Find the reflection of the points (3, 2) about y axis A ray of light is send along the line x 2y 8 = 0 After refracting across the line x y 1 = 0 it enters the opposite side after turning by 1 5 o away from the line x y 1 = 0, then the equation of the line along which the reflacted ray travel is Plot D ( − 2, − 5) on the When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places allthemmarvelfeels 1 0 Answers #1 91 5 Best Answer When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places allthemmarvelfeels Post New Answer 12 Online Users Top Users CPhillThis video demonstrates how to reflect a figure over the line y=x It shows two methods of reflecting over y=x The video shows how to count towards the y=x
Solution Can We Reflect This Point In This Line Geometry Of Equations Underground Mathematics
Reflection in the line y=x linear transformation
Reflection in the line y=x linear transformation-Solution for 2 The point (7,4) is reflected over the line x =3 Then, the resulting point is reflected over the line y x Where is the point located afterThe midpoint of XY is M(6, 5) If the coordinates of X are (3, 2), what are the coordinates of A Since you have asked multiple questions in single request so we will be answering only first quest question_answer Q 2 Point T is on line segment SU Given ST = 2x 6, TU = 4, and SU = 4x, determine the numerical le A Given T is a point on line segment SU ST = 2x6 TU = 4



Reflection Across Y 2 Silent Solution Youtube
Answer choices (4,0) (0,4) (0,4) (4,0) s Question 3 SURVEY 30 secondsMathematics Answer Comment 1 answer Effectus 21 1 year ago 4 0 Answer (7,2) Stepbystep explanation formula reflection in the line y=x M (x,y)=(x,y) Send You might be interested in Answer the three questions pls Mila 1 If you divide the cost by the ounces, that will be the unit rate 360 divided by 12 In this lesson we'll look at how the reflection of a figure in a coordinate plane determines where it's located A reflection is a type of transformation that flips a figure over a line The line is called the line of reflection, or the mirror line The line of reflection can be horizontal, vertical, or diagonal Hi!
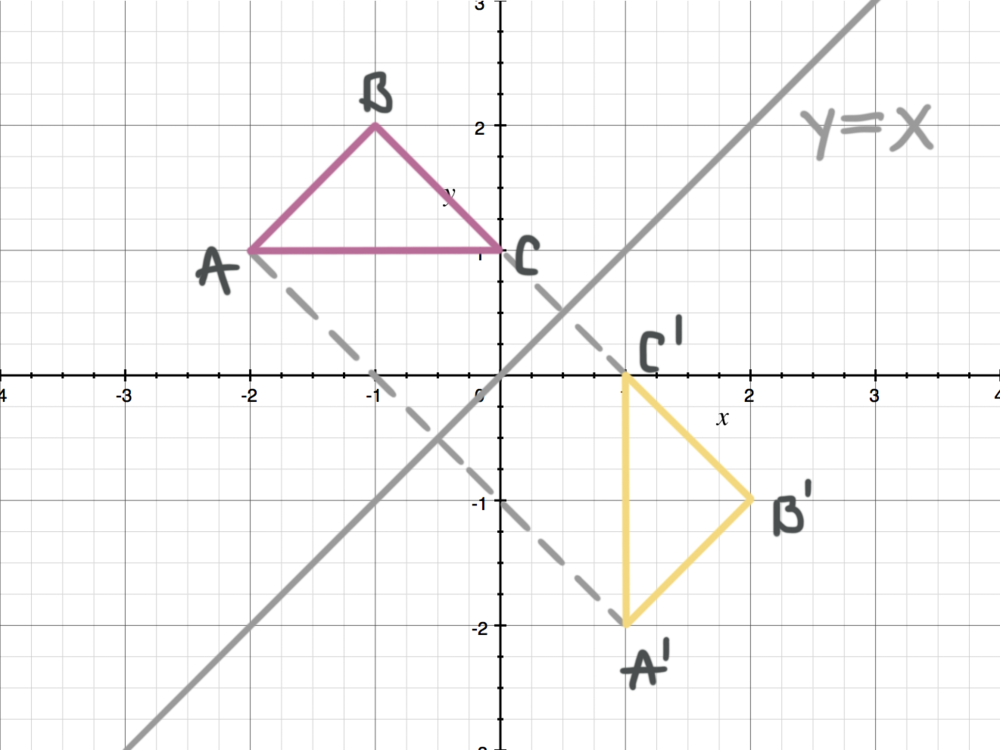
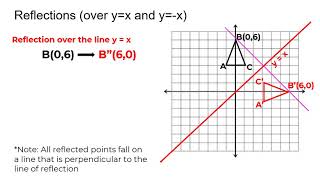
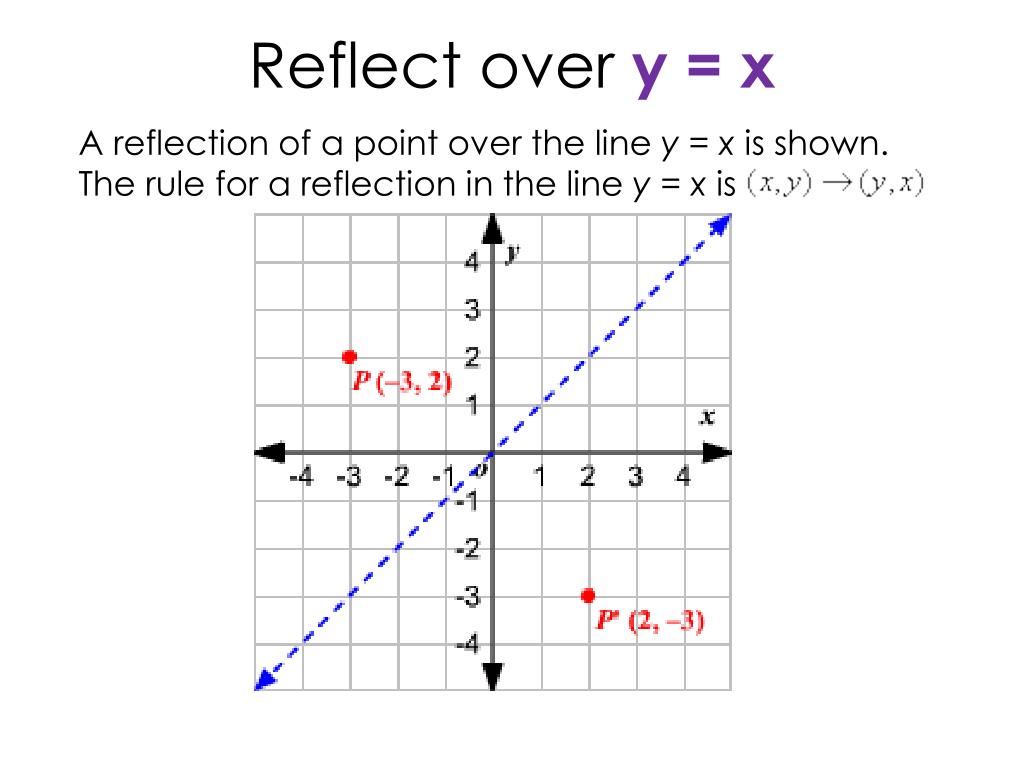
Advertisement Advertisement glasu is waiting for your help Add your answer and earn points curio curio Answer (2, 8) Stepbystep explanation All you need to do is swap the y and x value The rule for reflections across y = x is simply (y, x) Advertisement Advertisement New Let T R 2 → R 2 be a linear transformation that maps the line y = x to the line y = − x Note that the linear transformation T is completely determined if the values of T on basis vectors of the vector space R 2 are known Let B = { 1 0, 1 1 } The y = x reflection is a type of reflection on the Cartesian plane where the preimage is reflected with respect to the line of reflection with an equation of y = x Imagine a diagonal line passing through the origin, y = x reflection occurs when a point or a given object is reflected over this line Before diving deeper into the process of
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x What is the image of (8,1) after a reflection over the line y=x 1 See answer Advertisement Advertisement sofiapalma1010 is waiting for your help Add your answer and earn points jimrgrant1 jimrgrant1 Answer ( 1, 8 ) Stepbystep explanation Under a reflection in the line y = x a point (x, y ) → (y, x ) , thus (8, 1 ) → ( 1, 8 ) Advertisement Advertisement NewTutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT



How To Reflect Across The Line Y X



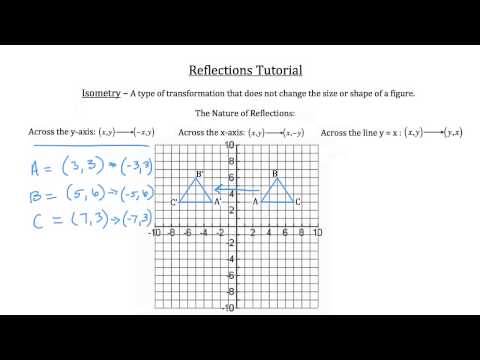
1
image A' = (5 , 3 ) Any point (x , y ) when reflected in the line y = x has an image ( y , x ) example A (3 , 4 ) has image A' ( 4 , 3 ) Precalculus Science Anatomy & Physiology Astronomy Astrophysics Biology Chemistry Earth Science Environmental Science Organic Chemistry Physics Math Algebra Calculus Geometry Prealgebra Precalculus Statistics TrigonometryA reflection of a point over the line y = − x is shown The rule for a reflection in the origin is ( x, y) → ( − y, − x)A) Rotation by 45 degrees counterclockwise followed by reflection in the line y = − x B) Projection in the line y = x 2 followed by rotation by 60 degrees clockwise I attempted part A, and these are my results R is the rotation, and F is the reflection R 45 c c w = 0 − 2 2 1 2 2 and F y = − x = 0 − 1 1 0 Then F y = − x




Graph The Image Of The Polygon After A Reflection In The Line Y X Please Help Brainly Com



Reflect Function About Y Axis F X Expii
Expert Solution Want to see the full answer?Check out a sample Q&A here See Solution Want to see this answer and more?SWBAT reflect an image over y=x




How To Reflect A Polygon Over A Horizontal Line Geometry Study Com



1
What is the image of (2,−4) after a reflection over the line y=x?After a reflection over the line y = x, (8, 11) is the image of point C What is the original location of point C?Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha




Reflection Over X Axis Y Axis Equations Examples Graph Video Lesson Transcript Study Com




Reflections Through The Axes And The Lines Y X And Y X Geogebra
What is the image of (7,−2) after a reflection over the line y=x?Relative to this basis, the matrix of the reflection is simply Y = ( 1 0 0 0 1 0 0 0 − 1) from which you can get Υ via a change of basis B Y B − 1 Note that rightmultiplication by Y just changes the sign of the third column of a matrix In your case, the equation of the plane immediately gives us the normal ( − 1, 1, 2) T– Let's Answer The World!



What Is The Image Of 8 7 8 7 After A Reflection Over The Line Y Xy X Quora




Reflection Mathbitsnotebook A1 Ccss Math
When a given point is reflected over a line the point only changes place but the distance between the point and the line remains same Let (x,y) be a point on the plane and y = x be a line on the planeWhat is the image of (4,3) (4,3) after a reflection over the line y=xy=−x? (4,1) after reflection over the yaxis would become color(red)(""(4,1)) A reflection over the yaxis leaves the point the same distance above the xaxis (that is the ycoordinate value does not change) The xcoordinate value becomes an equal distance from the yaxis but on the other side of the yaxis (that is the xcoordinate value becomes the negative of what it was)




Reflection Over X Axis Y Axis Equations Examples Graph Video Lesson Transcript Study Com




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
How to reflect shapes on a mirror line or x axis, y axis, coordinate grid, graph or even cartesian plane – it's all pretty much the same The biggest problem isn't really the reflection it's more making sure that you've correctly identified the 'mirror line' This can cause a few problems and a little confusion The easiest way is to actually plot a couple of points on the👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change size




Reflection Definition Reflection In The Coordinate Plane



Reflecting Figures In Coordinate Space Krista King Math Online Math Help
Part D Which point is a reflection of point K over the line y =− x?1 See answer Advertisement Advertisement bbrown777 is waiting for your help Add your answer and earn points jimrgrant1 jimrgrant1 Answer ( 4, 2 ) Stepbystep explanation Under a reflection in the line y = x a point (x, y ) → (y, x ), thus (2, 4 ) → ( 4, 2 ) Advertisement Advertisement New questions in0 0 Similar questions Consider two points A=(1,2) and B(3,−1)




Reflecting Shapes Article Reflections Khan Academy



Reflection Over The X And Y Axis The Complete Guide Mashup Math
To reflect the point over the y=x line, it's necessary to find the formula for the line which is perpendicular to y=x ( that would be y=xb) and which passes the given point (which affects the b constituent of the y=xb formula)A ray of light coming along the line 3 x 4 y − 5 = 0 gets reflected from the line a x b y − 1 = 0 and goes along the line 5 x − 1 2 y − 1 0 = 0 then Medium View solution > Which point is a reflection of point A over the line y = x?Students who viewed this also studied Hollywood Hills High School • AP Human Geog Section 3



Matrices As Transformations




Reflection In The Line Y X Geogebra
Check out a sample Q&A here See Solution Want to see the full answer? What is the image of (2,8) after a reflection over the line y = x?Preview (9 questions) Show answers Q The point ( 2,5) is reflected over the line x = 1 Find its image Q What is the image of T (4, 1) after a reflection over the Q What is the reflection of P (2, 6) over the line y = x



What Is The Reflection Over The Y Axis Of The Point 4 7 Quora




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
Vertical Reflection Apply a reflection over the line y=1 The procedure to determine the coordinate points of the image are the same as that of the previous example with minor differences that the change will be applied to the yvalue and the xvalue stays the same In the end, we would have A'(6,2), B'(5,7), and C'(5, 3) VideoLesson Transcript Let's say we want to reflectTo describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1\) is a vertical line which passes through 1 onPosted on 2 September 21 by lets tokmak



Reflection Over The Y X Line Youtube




If Triangle Xyz Is Reflected Across The Line Y 1 To Create Triangle X Y Z What Is The Ordered Brainly Com
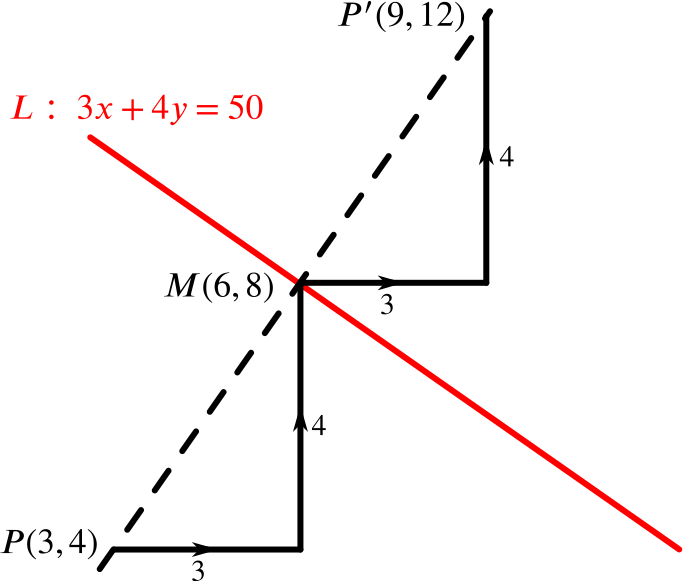
Reflect the shape below in the line y = −x StepbyStep 1 Find the Cartesian coordinates of each point on the shape Write the xcoordinates and ycoordinates of each point 2 Change the sign of both coordinates Make them negative if they are positive and positive if they are negative 3 What is the image of (8,5)(−8,−5) after a reflection over the line y=xy=x?Solution Verified by Toppr Correct option is D) Fundamental fact The reflection of any point (x,y) in the line y=x is given by (y,x) or the x and ycoordinate will be exchanged to each other Hence reflection of point (6,8) in the line x=y is (8,6) Was this answer helpful?




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs
Answer choices (11,8) (8, 11) (6, 11) (1,3) s Question 2 SURVEY 30 seconds Q After a reflection over the yaxis, (0,4) is the image of point L What is the original location of point L?Easy View solution > The reflection of the point (6, 8) in the line x = y is Medium View solution > A ray of light coming along the line 3x 4y 5Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!* See Answer *Response times may




Reflection Rules How To W 25 Step By Step Examples




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
File previews pdf, 975 KB Worksheet for students to use to reflect shapes in the x and y axes Also reflecting in the line y=x (diagonal line bottom left Homework Statement Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a SolutionPLS ANSWER FAST 2 See answers Advertisement Advertisement trubblebubble trubblebubble Answer 4,16 Stepbystep explanation Multiply each by 2 2 x 2 = 4 8 x 2 = 16 Advertisement Advertisement deanmizkun deanmizkun Ended up getting the answer wrong because the other person this is




Reflection Mathbitsnotebook A1 Ccss Math



What Is The Image Of 2 5 Reflected Across X 2 Socratic
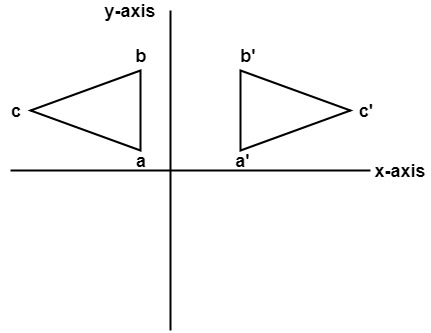
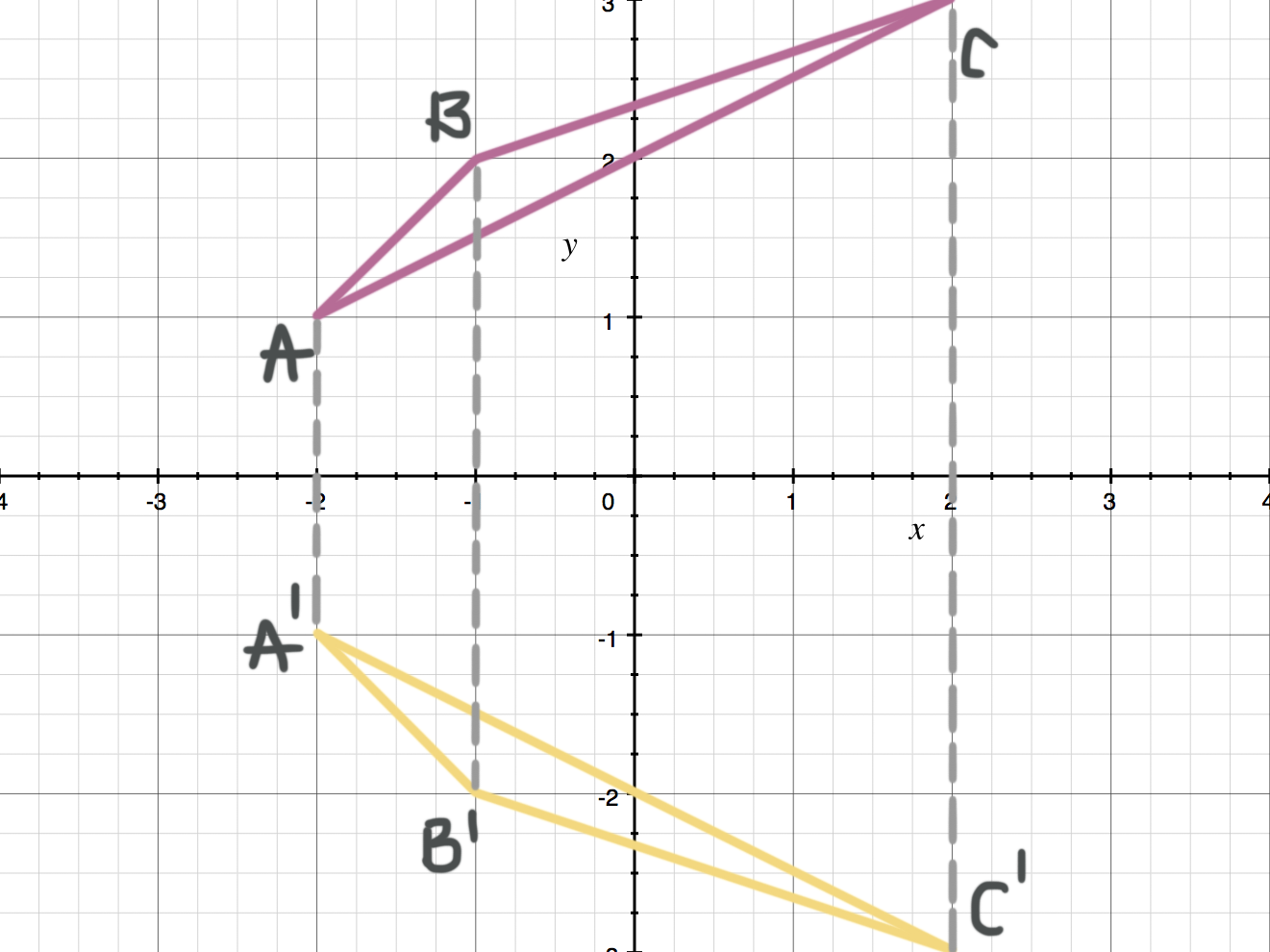
Reflecting over Any Line When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure In other words, the line x = 2 (line of reflection) lies directly in the middle between the original figure and its image And also, the line x = 2 (line of reflection To reflect over a vertical line, such as x = a, first translate so the line is shifted to the yaxis, then reflect over it, then translate back so the line is shifted to its original position In this case to reflex over x = − 1 we shift x ↦ x 1, reflect ↦ − 1 − x and shift back ↦ − 2 − x10 Consider the following graph Find the coordinates of figure A ' B' C ', the images of the vertices of figure ABC under the following reflections r x − axis r y − axis r y = x Share this link with a friend Copied!



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora



How To Reflect Across The Line Y X
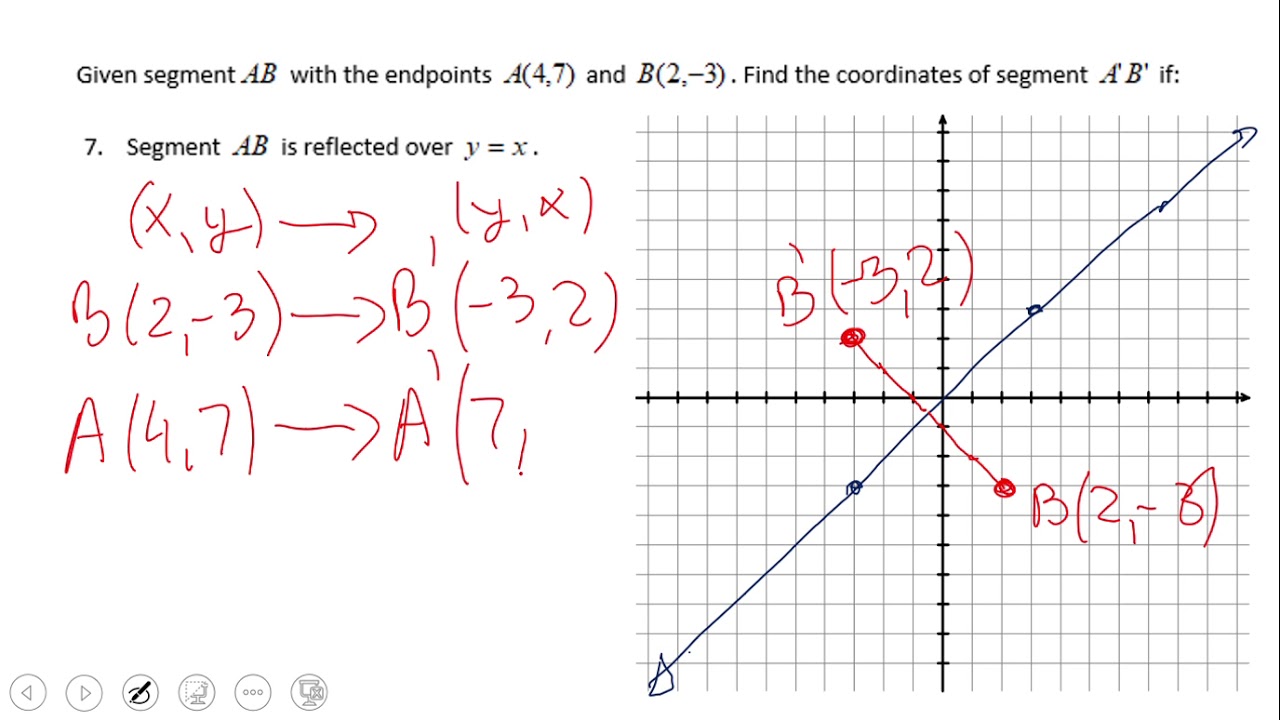
Answer (1 of 4) There are at least two ways of doing so Method 1 The line y = 3 is parallel to xaxis Let the required image is P′ By common sense, we know (Distance between the line y = 3 and point P) = (Distance between line y= 3 and point P′) Since line joining PP′ is perpendicular toWhat is the image of (9, 5) after a reflection over the line y = x?When we reflect a point in the xy plane over the line y = x, the image has the x and ycoordinates switched So here, (2, 5) and (5, 2) are reflected images of each other over the line y = x In other words, we swap the place of the xcoordinate and the ycoordinate, that's the effect of reflecting over this particular line



Computer Graphics Reflection Javatpoint



9 2 Reflections Objective To Find Reflection Images Of Figures Ppt Download
To reflect along a line that forms an angle θ with the horizontal axis is equivalent to rotate an angle − θ (to make the line horizontal) invert the y coordinate rotate θ back Further, y = m x implies tan θ = m, and 1 m 2 = 1 cos 2 What the image of ( 6, 5) after a reflection over the line y = x ?




Reflection Over The Y X Line Youtube



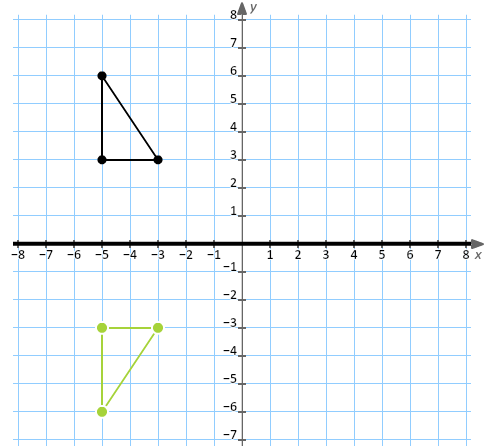
Reflecting Figures In Coordinate Space Krista King Math Online Math Help



Reflection In A Cartesian Plane Lexique De Mathematique
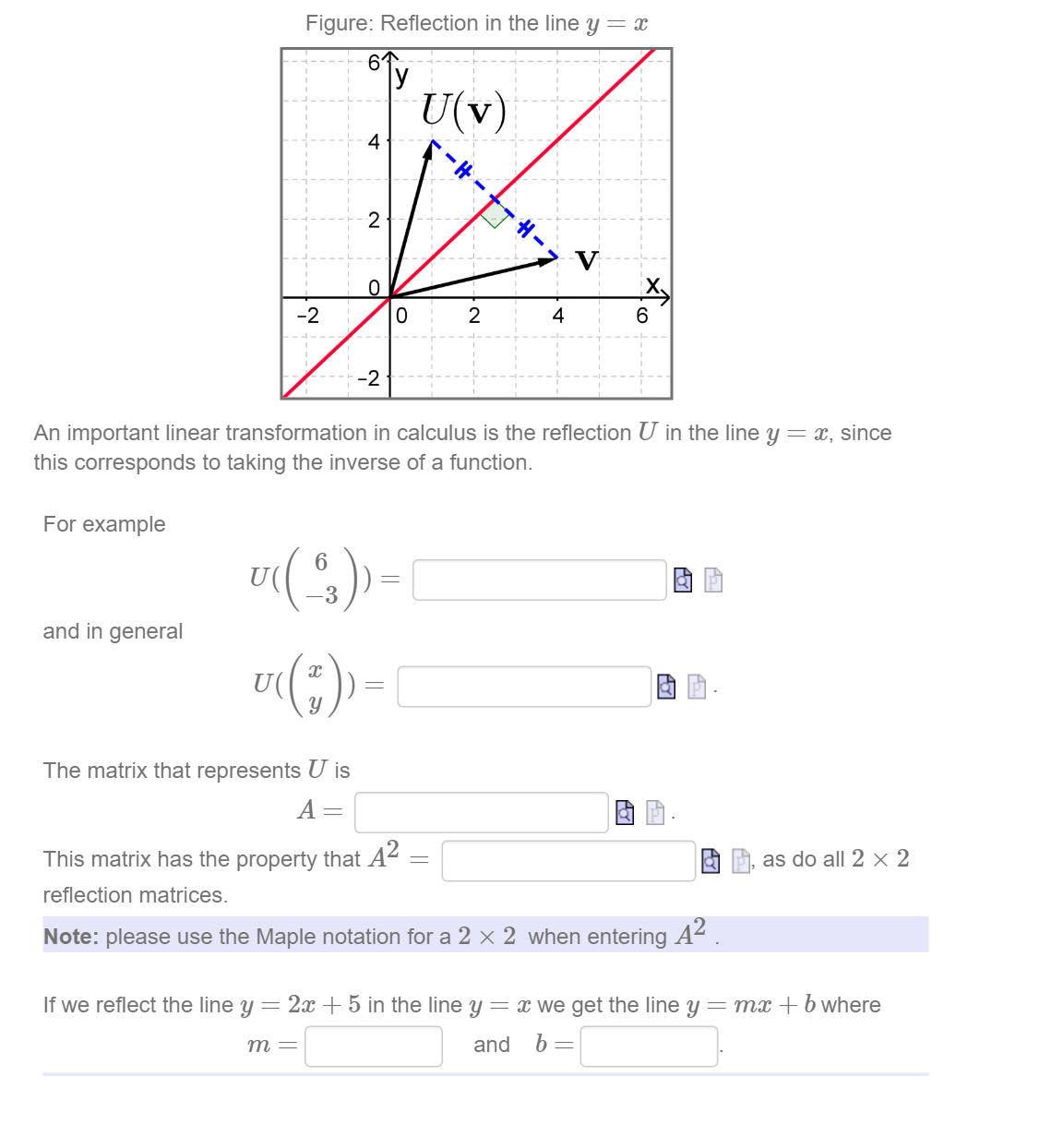



Solved An Important Linear Transformation In Calculus Is The Chegg Com




Reflection Across Y 2 Silent Solution Youtube




Common Reflections Key Stage 3
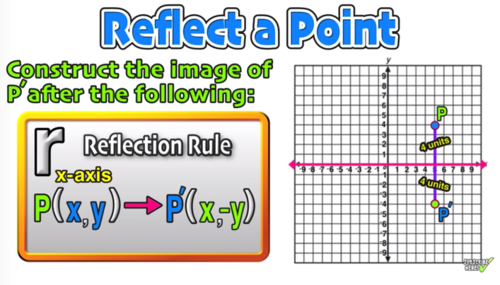



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Comparing And Explaining Transformations Texas Gateway




How To Reflect A Line Segment Across The X Axis Or Y Axis Geometry Study Com




Reflection Over Y X Math Geometry Showme



Reflection Over Y X And Y X Youtube



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
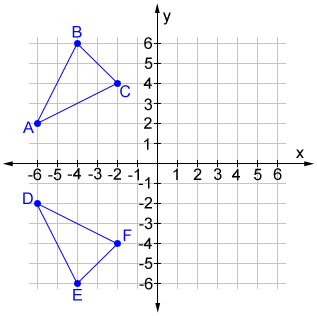



Reflection




Reflection In The Line Y X Transformation Matrix Youtube




Reflect Shape A In The Line Y X Brainly Com




Reflection Transformation




Reflecting Functions Examples Video Khan Academy



1




How To Find A Reflection Image
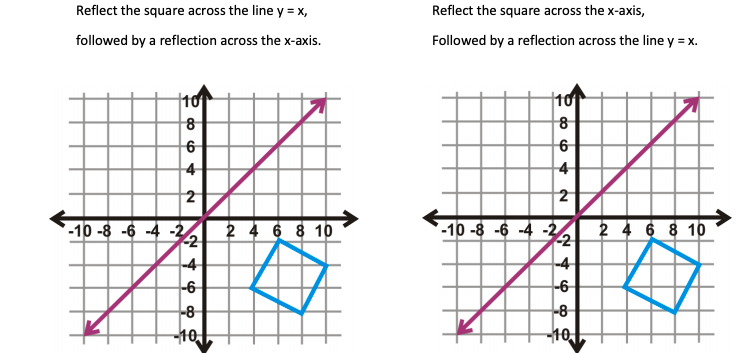



How To Reflect Across The Line Y X




Reflection Mathbitsnotebook A1 Ccss Math




Transformation Reflection Over The Line Y X Youtube



Translations And Reflections Activity Builder By Desmos




Triangle Jkl Is Translated Using X Y Gt X 1 Y 3 After It Is Reflected Across The Brainly Com




Learn About Reflection Over The Line Y X Caddell Prep Online



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor



Math Alive Geometry 1




The Image Of The Point 5 4 Under A Reflection Across The Y Axis Is 5 4




What Is The Image Of 5 6 5 6 After A Reflection Over The Line Y Xy X Brainly Com
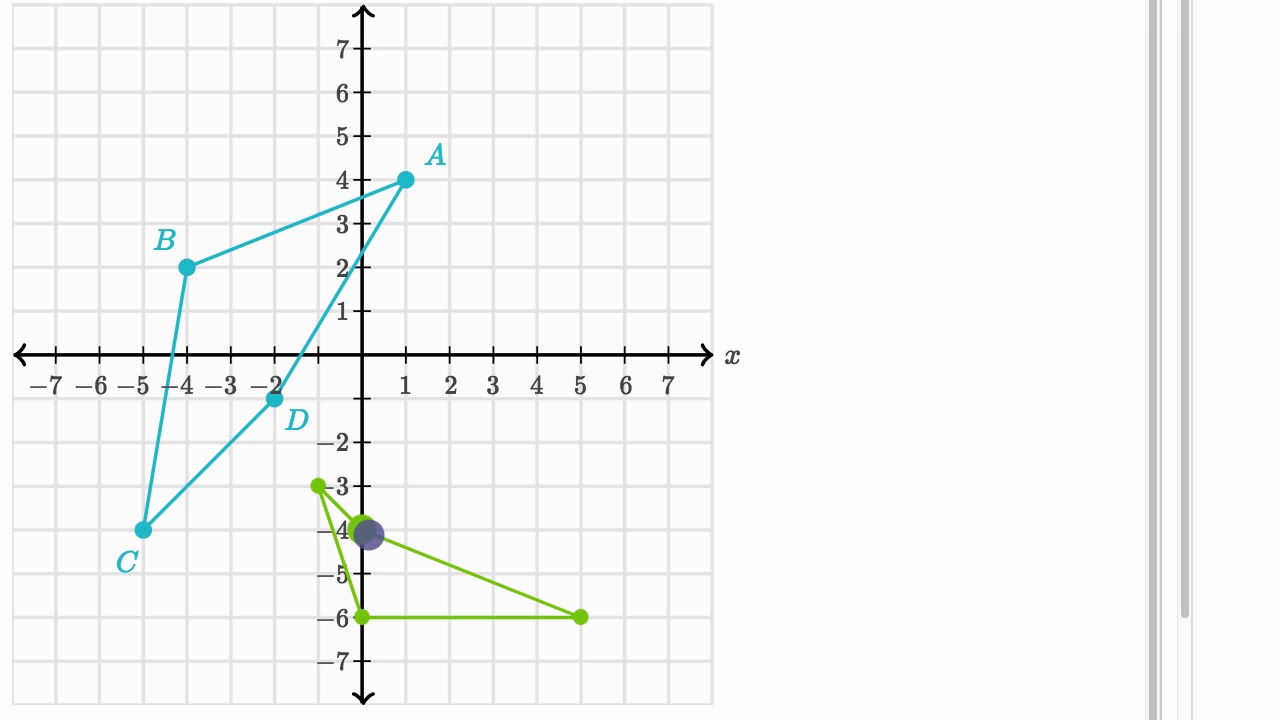



Reflecting Shapes Video Reflections Khan Academy



Reflect Points Over The X And Y Axes Learnzillion
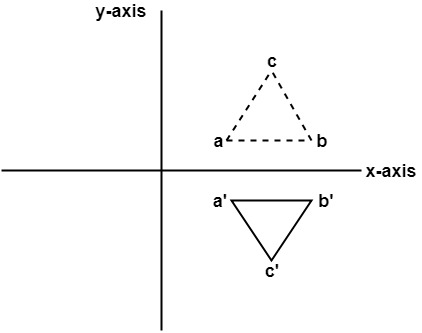



Computer Graphics Reflection Javatpoint




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflections Across Y X Geogebra



Reflection Of A Point In A Line Msrblog




Solution Can We Reflect This Point In This Line Geometry Of Equations Underground Mathematics



How To Find The Reflection Of A Line Over A Line Quora
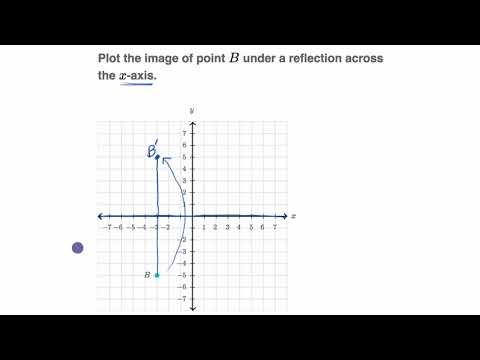



Reflecting Points Video Reflections Khan Academy




Reflection Mathbitsnotebook A1 Ccss Math




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



2




Reflecting In The Coordinate Plane




Reflections
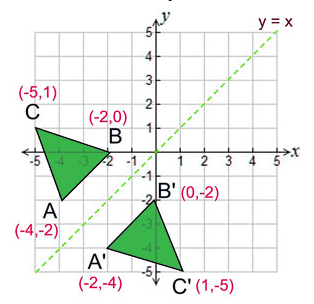



Reflection Definition Reflection In The Coordinate Plane
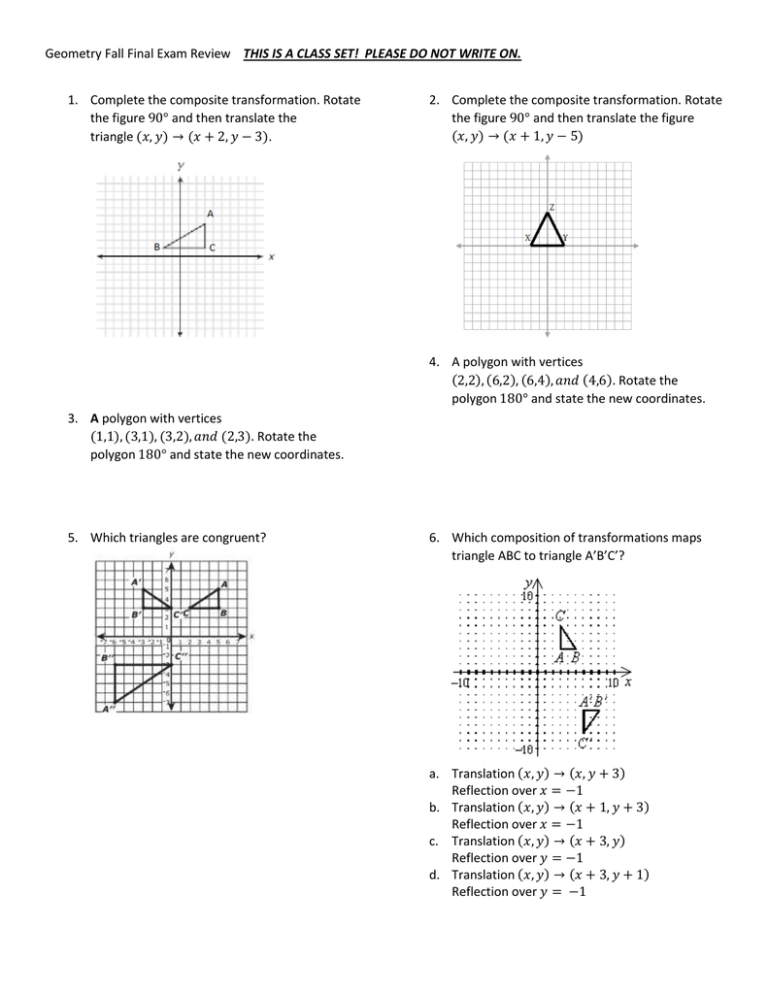



This Is A Class Set Please Do Not Write 1 Complete The Composite Transformation Rotate
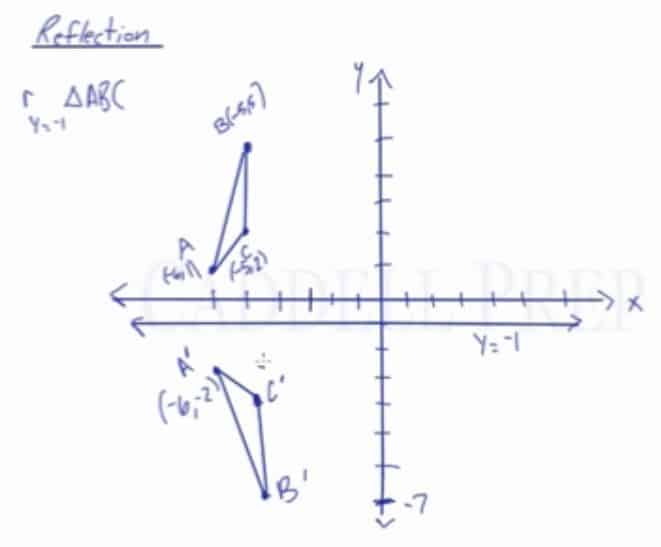



Learn About Reflection Over A Horizontal Or Vertical Line



How To Reflect Across The Line Y X



Reflection Across The Line Y X Geogebra




Graph Xy With Endpoints X 5 2 And Y 3 3 And Its Image After A Reflection In The X Axis And Then A Brainly Com




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
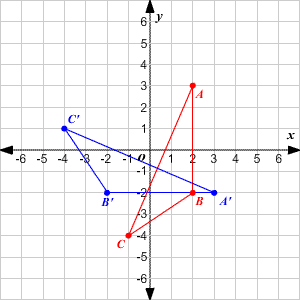



Transformations Of Graphs
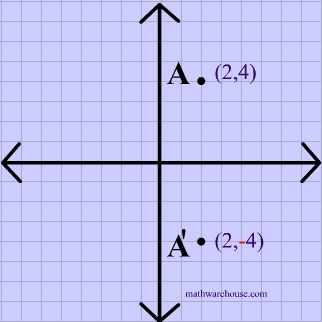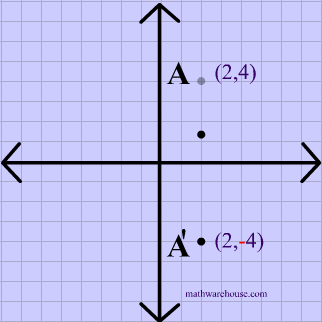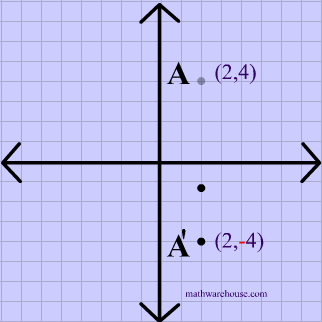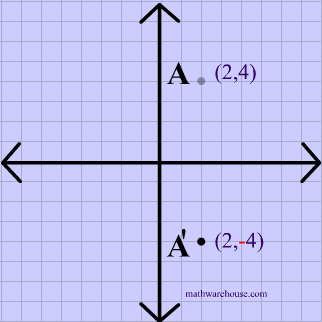



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Over A Line Expii




Reflections Day 1 Geogebra
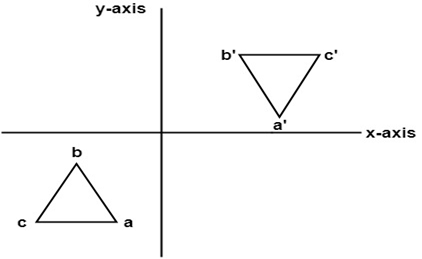



Computer Graphics Reflection Javatpoint
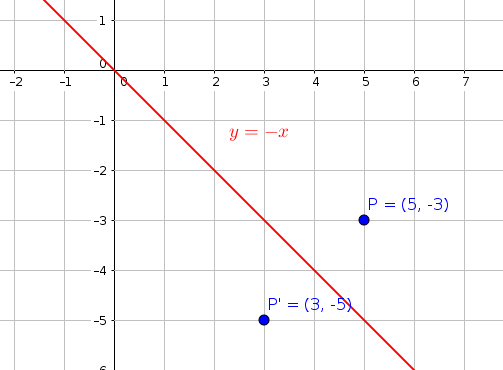



What Is The Reflection Image Of 5 3 In The Line Y X Socratic




Reflection Mathbitsnotebook A1 Ccss Math




Reflecting Figures In Coordinate Space Krista King Math Online Math Help



What Does It Mean To Reflect Over The Y X Line Quora




Reflection Over The Line Y X Geogebra




Reflection Over The Line Y X Youtube




Reflection Geometry Quiz Quizizz




Coordinate Geometry Reflections In The X Y Plane Youtube




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
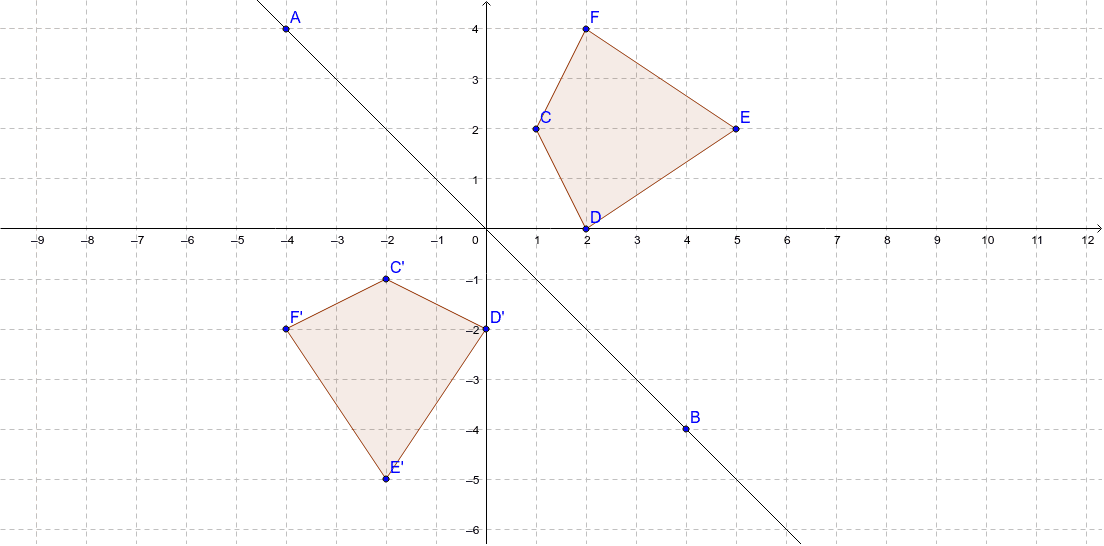



Reflection Over Y X Geogebra



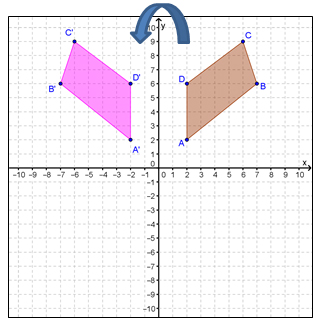
Rotation Rules



0 件のコメント:
コメントを投稿